Si expresamos este ciclo en una secuencia causal, tenemos lo siguiente:13. La lógica es un modelo deficiente de la causa y el efecto.
Utilizaremos las mismas palabras para referirnos a secuencias lógicas y a secuencias de causa y efecto. Decimos: "Si se aceptan las definiciones y postulados de Euclides, entonces dos triángulos que tengan sus tres lados iguales son iguales entre sí". Y también decimos: "Si la temperatura desciende por debajo de 0º C, entonces el agua se solidifica".
Pero los "si... entonces..." de la lógica del silogismo son muy distintos de los "si... entonces..."de la causa y el efecto.
En una computadora, que opera por causa y efecto, en la que un transistor pone en movimiento al otro, las secuencias de causa y efecto se emplean para simular la lógica. Hace treinta años solíamos preguntar: ¿Puede una computadora simular todos los procesos de la lógica? La respuesta era afirmativa, pero la pregunta era sin duda equivocada. Debería haber sido esta otra: ¿Puede la lógica, simular todas las secuencias de causa y efecto? Y la respuesta habría sido negativa.
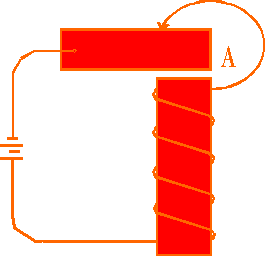
Cuando las secuencias de causa y efecto se vuelven circulares (o adquieren formas más complejas aún que la circular), la descripción o trazado de esas secuencias en la lógica atemporal se torna auto-contradictoria. Se generan paradojas que la lógica pura no puede tolerar. El circuito de un timbre ordinario nos servirá de ejemplo -una de las aparentes paradojas generadas en un millón de casos de homeostasis en toda la biología-. El circuito del timbre (véase la figura 3) está armado de modo tal que la corriente circula cuando la armadura hace contacto con el electrodo en A; pero el pasaje de corriente activa el electroimán que aparta a la armadura, haciendo cesar el contacto en A. La corriente deja entonces de circular por el circuito, el electroimán se desactiva, la armadura vuelve a hacer contacto en A, y el ciclo se repite.
Si expresamos este ciclo en una secuencia causal, tenemos lo siguiente:
Si se hace contacto en A, entonces se activa el electroimán.
Si se activa el electroimán, entonces cesa el contacto en A.
Si cesa el contacto en A, entonces se desactiva el electroimán.
Si se desactiva el electroimán, entonces se hace contacto.
Esta secuencia es perfectamente satisfactoria siempre y cuando quede bien en claro que las combinaciones "si... entonces... " son causales. Pero si se quiere hacer una mala broma y pasar los "si" y los "entonces" al mundo de la lógica, el resultado será escandaloso:
Si se hace contacto, entonces cesa el contacto.
Si P, entonces no P.
Los "si... entonces..." de la causalidad contienen tiempo, mientras que los "si... entonces..." de la lógica son atemporales. De esto se desprende que la lógica es un modelo incompleto de la causalidad.