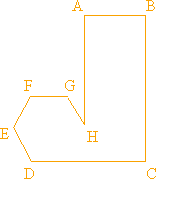
Figura 1.
5. La división del universo percibido en partes y tonalidades es conveniente y puede ser necesaria, [iv] pero ninguna necesidad determina de qué modo debe practicársela.

Muchas veces he intentado enseñar esta generalidad a grupos de estudiantes, utilizando para ello la figura 1. Esta figura se presenta a la clase dibujándola con tiza sobre el pizarrón con bastante precisión, pero sin colocar las letras que señalan los diversos ángulos. Se pide a la clase que describa "eso" por escrito. Cuando todos terminan su descripción, se comparan los resultados. Estos se clasifican en diversas categorías:
a. Alrededor de un diez por ciento de los estudiantes, o menos, dicen, verbigracia, que el objeto es una bota, o, más graciosamente, la bota de un hombre con un dedo gotoso o aún inflamado. Es evidente que partiendo de descripciones analógicas o icónicas como esta le seria difícil al que oyera la descripción reproducir el objeto.
b. Un número mucho mayor de estudiantes ven que el objeto contiene la mayor parte de un rectángulo y la mayor parte de un hexágono, y habiendo dividido la totalidad de esta manera se aplican luego a describir las relaciones entre el rectángulo y el hexágono incompletos.
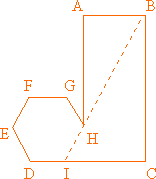
Un pequeño número de integrantes de este grupo de alumnos (aunque por lo común, sorprendentemente, uno o dos en cada clase) descubren que puede trazarse una línea, BH, hasta que corte la base DC en un punto I, de modo tal que HI complete un hexágono regular (figura 2). Esta línea imaginaria definirá las proporciones del rectángulo, aunque no, desde luego, la longitud de sus lados en términos absolutos. Suelo felicitar a estos estudiantes por su capacidad para crear lo que se asemeja a muchas hipótesis científicas, que "explican" una regularidad perceptible en función de alguna entidad creada por la imaginación.
c. Muchos estudiantes bien entrenados recurren a un método operativo de descripción. Parten de algún punto del diagrama (cosa curiosa, casi siempre es un ángulo) y siguen, por lo general en el sentido de las agujas del reloj, dando las instrucciones para dibujar el objeto.
d. Hay otras dos modalidades de descripción bien conocidas que hasta la fecha ningún estudiante empleó. Ninguno partió del enunciado: "Está hecho de tiza y pizarrón". Ninguno utilizó jamás el método del grabado de media tinta, dividiendo la superficie del pizarrón en un reticulado (arbitrariamente rectangular) y respondiendo luego "si" o "no" según que cada cuadrícula contenga o no contenga una parte del objeto. Naturalmente, si el reticulado es muy grosero y el objeto es pequeño se perderá una gran cantidad de información. (Imagínese el caso de que el objeto entero sea más pequeño que una cuadrícula del reticulado; la descripción constará entones de no más de cuatro afirmaciones ni menos de una, según cómo caigan sobre el objeto las divisiones del reticulado.) No obstante, esta es, en principio, la manera en que trasmiten, mediante impulsos eléctricos, las medias tintas de una ilustración de periódico, y también es la manera como opera la televisión.
Repárese en que ninguno de estos métodos descriptivos contribuye en nada a una explicación del objeto -el hexágono rectángulo-. La explicación debe nacer siempre de la descripción, pero la descripción de la que nace contendrá siempre, necesariamente, características arbitrarias como las que hemos ejemplificado aquí.